Butterworth Filter

Overview

This metric applies a the SAE standard Butterworth filter at specified channel frequency classes (CFC). A Butterworth Filter works to filter data and create a steady signal frequency in the range of acceptable signals, specified by the user, while removing any interference in the signals.

Required Inputs

• Time History Signal
• Select desired CFC for signal:
  • 60, 180, 600, or 1000 Hz

Calculation

1. Convert time units to seconds
2. Calculate sampling rate (T) based on time difference between two consecutive data points
3. Adds data to the ends of signal if there is not enough padding present
4. Calculate filter coefficients using selected cutoff frequency and SAE J2111 standards for bandwidth filters

$$Angular\,Frequency\,(wd) = 2pi*filter class*2.0775$$ $$Normalized\,Angular\,Frequency\,(wa) = \frac{sin(wd*(T/2))}{cos(wd*(T/2))}$$ $$Denominator\,Coefficients = \begin{cases} a0 = \frac{wa^2}{1+\sqrt(2)*wa+wa^2} \\ a1 = 2*a0 \\ a2 = a0\end{cases}$$ $$Numerator\,Coefficients = \begin{cases} b0 = 1 \\ b1 = \frac{-2(wa^2-1)}{1+\sqrt(2)*wa+wa^2} \\ b2 = \frac{-1+ \sqrt(2)*wa-wa^2}{1+\sqrt(2)*wa+wa^2}\end{cases}$$

5. Filter is applied both forward and backward (for minimal phase distortion) using filter coefficients (a0, a1, a2) and (b0, b1, b2) to compute the filtered signal

Butterworth Filter

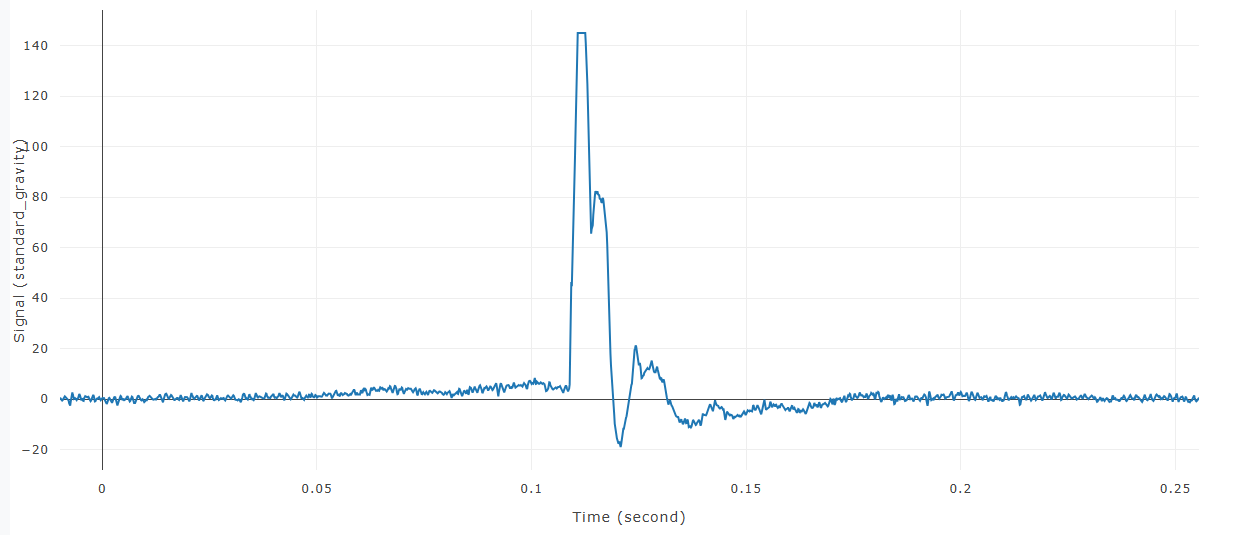
Before Butterwoth Filter is applied to the signal

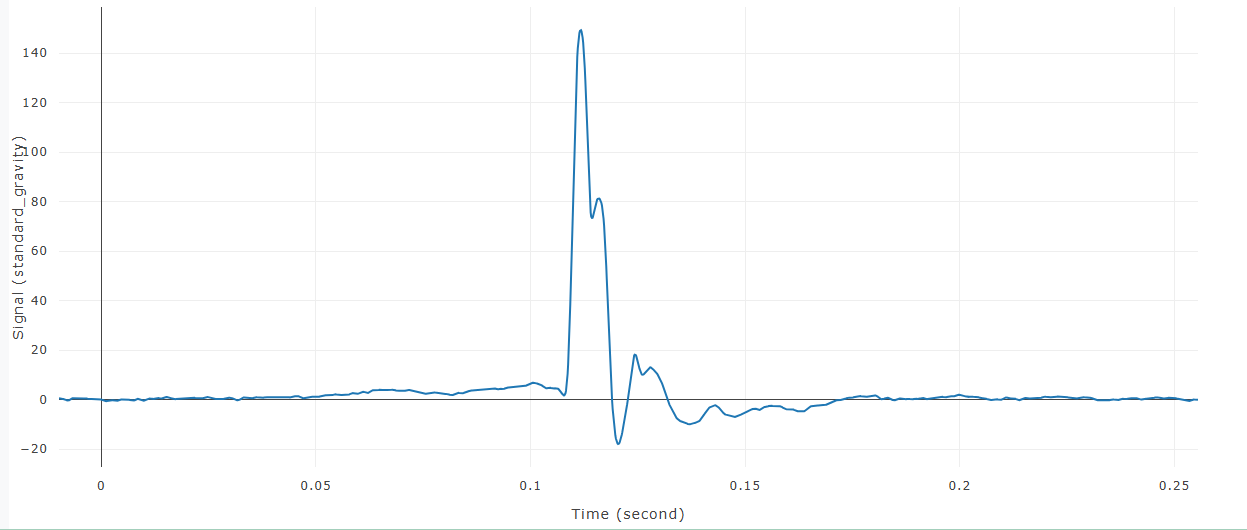
After Butterworth Filter is removed from signal