Skip to main content

Integrate

Overview​

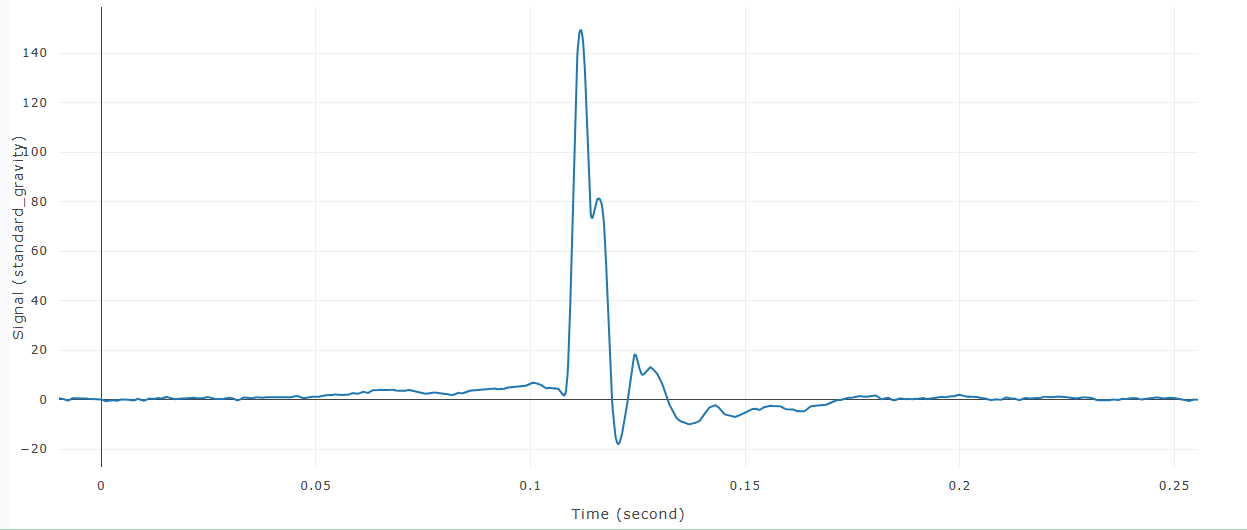
This test metric calculates the area under a curve of a specified signal using the trapezoid rule.

Required Inputs​

  • Time History Signal

Calculation​

  1. Converts signal's time unit and data units to be harmonious
  2. Initial value is removed from integration and the difference between the initial value and integral value at time = 0 seconds is added to the calculated areas (Step 3)
  3. Calculate area under curve at each data point, starting at the second data point
    • Area between data points calculated using the trapezoid rule (equation below)

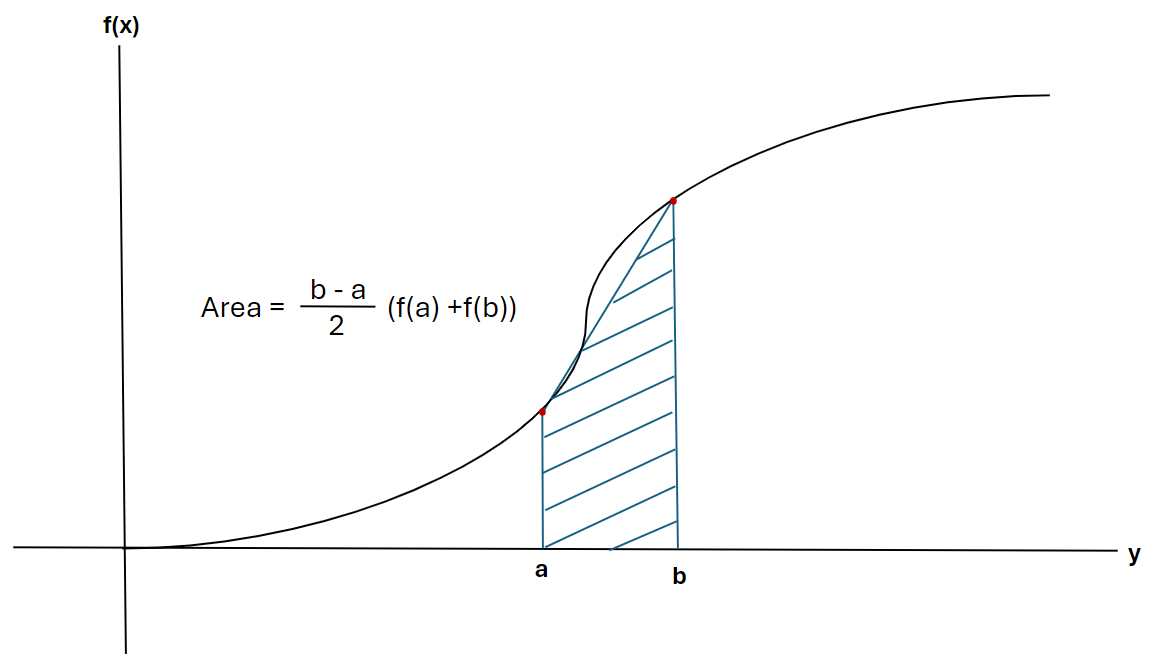
Integration area

Area under curve between points a and b

  1. Add together all calculated areas to find signal's integral

Equation​

∫abf(x)dx=b−an[f(xinital)+2f(x2)+2f(x3)+2f(x4)....+f(xlast)]\int_a^b f(x)dx = \frac{b-a}n[f(x_{inital}) + 2f(x_{2}) + 2f(x_{3}) +2f(x_{4}).... +f(x_{last})]

Integrate Example​

Before integrate

Before signal is integrated

After integrate

After signal is integrated